How to Use Chord Formulas and Their Benefits

September 4, 2023 by Klaus Crow

Why do you need chord formulas? Why do want to learn about them in the first place and what are their benefits?

Knowing some basic chord theory can make all the difference to your playing. It makes guitar playing more fun, interesting and a lot of what you play will make more sense. The pieces of the puzzle will fall in place.

Knowing how chord formulas work and knowing the notes on the strings is the ultimate combination.

What can you do with chord formulas?

– Learn how to make your own chords.
– Understand music theory.
– Figure out how to play a chord when you only have the name of a chord.
– Understanding the difference between chords like Dom7, Maj7 and min7.
– Make a chord easier to play if your pinky can’t reach for the major 7 or any other nasty note.
– Quickly turn a G major chord into Gsus4, G7, Gmaj7, G13 or any other variation you think of.
– Learn to see how easy it is to change from major to minor or any other chord.
– Apply the knowledge to your rhythm playing, songwriting, soloing and improvisation.
– Discover how chord formulas relate to every aspect of guitar playing as your knowledge expands over time.

What is a Chord Formula?

Chord formulas reveals the chord structure. It shows all the notes that are played in a chord, in other words, which specific notes make up a particular chord.

The notes in a chord are taken from the major scale.
The notes of the major scale are referred to as numbers 1 2 3 4 5 6 7 and 8 (=1)

Example:
The notes below are from the C major scale referred as number 1 through 8.

C D E F G A B C
1 2 3 4 5 6 7 8 

From 8 the notes repeat only an octave higher: 8, 9, 10, 11, 12 and 13.
8 = 1 (C)
9 = 2 (D)
10 = 3 (E)
11 = 4 (F)
12 = 5 (G)
13 = 6 (A)

Here below you can pick a major scale key for the chords we’re going to build in the next section.

Major Scales in Every Key:

A major scale = A B C# D E F# G# A
Bb major scale = Bb C D Eb F G A Bb
B major scale = B C# D# E F# G# A# B
C major scale = C D E F G A B C
Db major scale = Db Eb F Gb Ab Bb C Db
D major scale = D E F# G A B C# D
Eb major scale = Eb F G Ab Bb C D Eb
E major scale = E F# G# A B C# D# E
F major scale = F G A Bb C D E F
Gb major scale = Gb Ab Bb Cb (=B) Db Eb F Gb
G major scale = G A B C D E F# G
Ab major scale = Ab Bb C Db Eb F G Ab

Building a Major Chord

To build a chord we need the chord formula and the major scale. Let’s build a C major chord.

The chord formula for a Major chord = 1 – 3 – 5
C major scale = C D E F G A B C

Now take the 1st, 3rd and 5th note of the major scale. Playing these notes simultaneously will result in a major chord. That means a C major chord consists of the notes: C E G (1 – 3 – 5)

You might wonder, “How can you hear only three notes when there are six strings on the guitar?” Well some notes in a chord appear twice. When you strum a C major chord you hear the following notes from the low E-string all the way to the high E-string.:

Low E string = mute
A string = C note
D string = E note
G string = G note
B string = C note
high E-string = E note

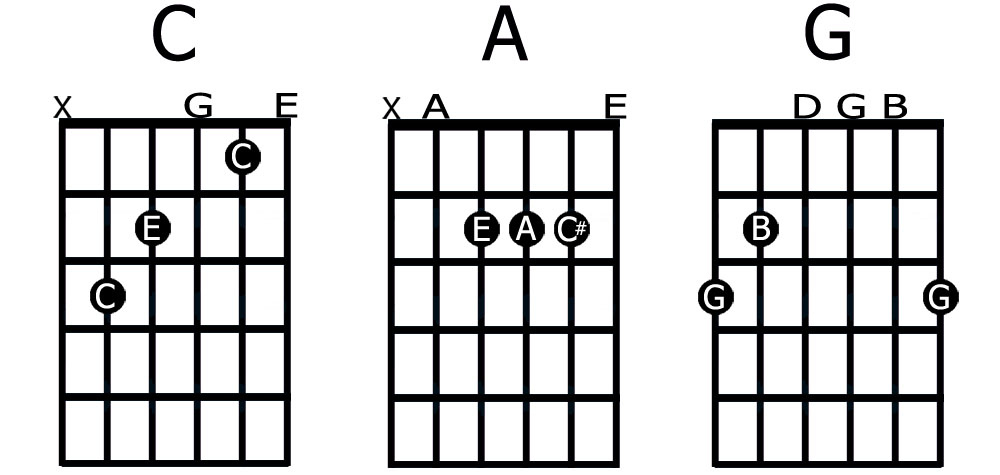
Check out some other major chord examples:
A major scale = A B C# D E F# G# A
A major chord = A C# E (1 – 3 – 5)

G major scale = G A B C D E F# G
G major chord = G B D (1 – 3 – 5)

The chord diagrams below show where notes are on the strings:

Building a Minor Chord

Let’s take the A minor chord for this example.

The chord formula for a Minor chord = 1 – b3 – 5.
A major scale = A B C# D E F# G# A

b3 (flat three) means you take the third note of the major scale only a half step down. The third note of the A major scale is C#, so if you go down a half step C# becomes C. That means the notes of the A minor chord consists of the notes A C E (1 – b3 – 5)

Building a Maj7 Chord

One last example: Gmaj7
G major scale = G A B C D E F# G
Maj7 chord formula = 1 – 3 – 5 – 7
Gmaj7 = G B D F#

List of Chord Formulas

Below you can see the most common chords and their chord formulas. I’ve taken the C root as example for all the chord names.

Chord name = chord formula | C root + chord name

Common Chord Types:

Major = 1 – 3 – 5 | C or Cmaj
Minor = 1 – b3 – 5 | Cm, Cmin, C-
Suspended Second = 1 – 2 – 5 | Csus2
Suspended Fourth = 1 – 4 – 5 | Csus4
Added ninth = 1 – 3 – 5 – 9 | Cadd9
Dominant Seventh = 1 – 3 – 5 – b7 | C7, Cdom7
Major Seventh = 1 – 3 – 5 – 7 | Cmaj7
Minor Seventh = 1 – b3 – 5 – b7 | Cm7, Cmin7, C-7

Major Chord Formulas:

Major = 1 – 3 – 5 | C or Cmaj
Major Sixth = 1 – 3 – 5 – 6 | C6, Cmaj6
Six Nine = 1 – 3 – 5 – 6 – 9 | C6/9
Added ninth = 1 – 3 – 5 – 9 | Cadd9
Major Seventh = 1 – 3 – 5 – 7 | Cmaj7
Major Seventh Flat Five = 1 – 3 – b5 – 7 | Cmaj7b5
Major Seventh Sharp Five = 1 – 3 – #5 – 7 | Cmaj7#5
Major Ninth = 1 – 3 – 5 – 7 – 9 | Cmaj9
Major Eleventh = 1 – 3 – 5 – 7 – (9) – 11 | Cmaj11
Major Thirteenth = 1 – 3 – 5 – 7 – (9) – (11) – 13 | Cmaj13
Major Seven Sharp Eleventh = 1 – 3 – 5 – 7 – #11 | Cmaj7#11
Major Flat Five = 1 – 3 – b5 | Cb5

Minor Chord Formulas:

Minor = 1 – b3 – 5 | Cm, Cmin, C-
Minor Sixth = 1 – b3 – 5 – 6 | Cm6, Cmin6, C-6
Minor Seventh = 1 – b3 – 5 – b7 | Cm7, Cmin7, C-7
Minor Added Ninth = 1 – b3 – 5 – 9 | Cmadd9
Minor Six Add Nine = 1 – b3 – 5 – 6 – 9 | Cm6/9
Minor ninth = 1 – b3 – 5 – b7 – 9 | Cm9
Minor eleventh = 1 – b3 – 5 – b7 – (9) – 11 | Cm11
Minor thirteenth = 1 – b3 – 5 – b7 – (9) – (11) – 13 | Cm13
Minor Major Seventh = 1 – b3 – 5 – 7 | Cm(Maj7)
Minor Major Ninth = 1 – b3 – 5 – 7 – 9 | Cm(Maj9)
Minor Major Eleventh = 1 – b3 – 5 – 7 – (9) – 11 | Cm(Maj11)
Minor Major Thirteenth = 1 – b3 – 5 – 7 – (9) – (11) – 13 | Cm(Maj13)
Minor Seven Flat Five = 1 – b3 – b5 – b7 | Cm7b5

Dominant Chord Formulas:

Dominant Seventh = 1 – 3 – 5 – b7 | C7, Cdom7
Ninth = 1 – 3 – 5 – b7 – 9 | C9
Elventh = 1 – (3) – 5 – b7 – (9) – 11 | C11
Thirtheenth = 1 – 3 – 5 – b7 – (9) – (11) – 13 | C13
Seven Sharp Five = 1 – 3 – #5 – b7 | C7#5
Seven Flat Five = 1 – 3 – b5 – b7 | C7b5
Seven Flat Ninth = 1 – 3 – 5 – b7 – b9 | C7b9
Seven Sharp Ninth = 1 – 3 – 5 – b7 – #9 | C7#9
Nine Sharp Five = 1 – 3 – #5 – b7 – 9 | C9#5
Nine Flat Five = 1 – 3 – b5 – b7 – 9 | C9b5
Seven Sharp Five Sharp Nine = 1 – 3 – #5 – b7 – #9 | C7#5#9
Seven Sharp Five Flat Nine = 1 – 3 – #5 – b7 – b9 | C7#5b9
Seven Flat Five Sharp Nine = 1 – 3 – b5 – b7 – #9 | Cb5#9
Seven Flat Five Flat Nine = 1 – 3 – b5 – b7 – b9 | C7b5b9
Seven Sharp Eleven = 1 – 3 – 5 – b7 – #11 | C7#11

Other Chord Formulas:

Diminished = 1 – b3 – b5 | Cdim
Diminished Seventh = 1 – b3 – b5 – bb7 | Cdim7
Half diminished = 1 – b3 – b5 – b7 | Cm7b5
Suspended Seventh = 1 – 4 – 5 – b7 | C7sus4, C7sus
Augmented = 1 – 3 – #5 | Caug, C+
Augmented Seventh = 1 – 3 – #5 – b7 | Caug7, C7#5, C7+
Fifth, Power Chord = 1 – 5 | C5
Flat Fifth = 1 – b5 | Cb5, C-, C-5
Suspended Second = 1 – 2 – 5 | Csus2
Suspended Fourth = 1 – 4 – 5 | Csus4

Assignments

1 – What are the notes of an Am7 chord?
(Use the A major scale and Minor Seventh formula)

2 – Draw an Am7 chord diagram and write down the notes that are played on each string.
(check the most common types of 7th chords)

3 – Check if the notes from the chord formula and the notes in the chord diagram correspond.

4 – Now build a G diminished seventh chord.(Go through steps 1 to 3)

5 – Play a random chord on your guitar. Use the appropriate chord formula and check
if all the notes from the chord on your guitar correspond with the notes from the chord formula.

5 – Write down the difference between a major chord and a minor chord formula?

6 – Write down the formulas for a Maj7, Dom7 and Min7 chord.
What they have in common and what are their differences?

7 – Start with memorizing the formulas common chord types.

Enjoy building your chords!

📨 Hi there, Join Guitarhabits and receive Free Quality Guitar Video Lessons, Top Content, Tips, Tricks, Resources & (bi)Weekly Guitarhabits’ Backpack Email full of good stuff. 🎸🎁  
SIGN UP HERE: https://www.guitarhabits.com/sign-up-guitarhabits/  
Support Guitarhabits here: https://www.guitarhabits.com/donate/